Hledej
Zobraz:
Univerzity
Kategorie
Rozšířené vyhledávání
12 662
projektů
Modelování dynamických systémů v ekonomice
| Přípona .doc |
Typ přednášky |
Stažené 1 x |
| Velikost 1,2 MB |
Jazyk český |
ID projektu 6613 |
| Poslední úprava 21.09.2015 |
Zobrazeno 1 517 x |
Autor: jiri.hosko |
 Sdílej na Facebooku
Sdílej na Facebooku |
||
| Detaily projektu | ||
- Cena:
2 Kreditů - kvalita:
89,3% -
Stáhni
- Přidej na srovnání
- Univerzita:Vysoká škola báňská - Technická univerzita Ostrava
- Fakulta:Fakulta ekonomická
- Kategorie:Ekonomika » Ekonomie
- Předmět:Matematika v ekonomii
- Studijní obor:-
- Ročník:1. ročník
- Formát:MS Office Word (.doc)
- Rozsah A4:22 stran
Systémová dynamika jako jedna z oblastí aplikací matematiky byla ustanovena v létech 1940 až 1950 a od té doby dosáhla řadu pozoruhodných úspěchů jakožto nástroj, s jehož pomocí lze pochopit dynamiku v chování složitých, strukturovaných systémů, které se vyvíjejí v čase. Aplikace systémové dynamiky jsou obsaženy v desítkách monografií, metod systémové dynamiky se s úspěchem používá pro analýzování chování složitých systémů v řadě zemí..
Za zakladatele metod systémové dynamiky a jejich aplikací lze považovat J.W.Forrestera [Fo], který publikoval řadu knih z této oblasti. Metody systémové dynamiky se posléze ukázaly jako velmi prospěšné při analýzování makrosystémů, jejichž chování v čase je ovlivněno řadou faktorů, které se navzájem ovlivňují. Celý proces aplikace těchto metod je značně komplikovaný a obtížný, proto se v této kapitole zaměříme pouze na vysvětlení některých jeho základních aspektů a pokusíme se ilustrovat tyto zjednodušené postupy na příkladech.
Tvorba dynamickým modelů není samoúčelný proces. Jeho hlavním cílem je získat nástroje pro analýzování chování složitých systémů měnících se v čase, u kterých nelze z praktických důvodů provádět experimenty. Nemožnost provádět experimenty je tedy jeden z hlavních rozdílů mezi dynamickými systémy popisujícími např. fyzikální procesy na jedné straně a např. ekonomické procesy na straně druhé.
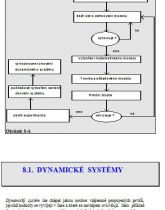
Celý proces tvorby a následného využívání dynamického systému můžeme stručně znázornit následujícím diagramem (obr. 8-1) Z tohoto schématu je vidět, že proces modelování dynamických systémů a následná práce s těmito modely je dosti komplikovaná záležitost. V této kapitole se proto budeme zabývat pouze vybranými problémy z této oblasti , týkajícími se zejména otázky tvorby matematického modelu dynamického systému.
Za zakladatele metod systémové dynamiky a jejich aplikací lze považovat J.W.Forrestera [Fo], který publikoval řadu knih z této oblasti. Metody systémové dynamiky se posléze ukázaly jako velmi prospěšné při analýzování makrosystémů, jejichž chování v čase je ovlivněno řadou faktorů, které se navzájem ovlivňují. Celý proces aplikace těchto metod je značně komplikovaný a obtížný, proto se v této kapitole zaměříme pouze na vysvětlení některých jeho základních aspektů a pokusíme se ilustrovat tyto zjednodušené postupy na příkladech.
Tvorba dynamickým modelů není samoúčelný proces. Jeho hlavním cílem je získat nástroje pro analýzování chování složitých systémů měnících se v čase, u kterých nelze z praktických důvodů provádět experimenty. Nemožnost provádět experimenty je tedy jeden z hlavních rozdílů mezi dynamickými systémy popisujícími např. fyzikální procesy na jedné straně a např. ekonomické procesy na straně druhé.
Celý proces tvorby a následného využívání dynamického systému můžeme stručně znázornit následujícím diagramem (obr. 8-1) Z tohoto schématu je vidět, že proces modelování dynamických systémů a následná práce s těmito modely je dosti komplikovaná záležitost. V této kapitole se proto budeme zabývat pouze vybranými problémy z této oblasti , týkajícími se zejména otázky tvorby matematického modelu dynamického systému.
Klíčová slova:
dynamické systémy
konstrukce
diagramy
proudové diagramy
matematický model
Obsah:
- 8.1 . Dynamické systémy 4
8.2 . Matematický model spojitých sýstémů 7
8.2.1 . Dynamický systém 7
8.2.2 . Příklad dynamického systému 10
8.3 . Konstrukce dynamických modelů 12
8.3.1 . Kauzální diagramy 12
8.3.2 . Proudové diagramy 16
8.3.3 . Matematický model 19