Hledej
Zobraz:
Univerzity
Kategorie
Rozšířené vyhledávání
12 662
projektů
Matematický seminář
| Přípona |
Typ skripta |
Stažené 1 x |
| Velikost 0,8 MB |
Jazyk český |
ID projektu 3981 |
| Poslední úprava 18.08.2014 |
Zobrazeno 1 133 x |
Autor: eliskabila |
 Sdílej na Facebooku
Sdílej na Facebooku |
||
| Detaily projektu | ||
- Cena:
8 Kreditů - kvalita:
79,8% -
Stáhni
- Přidej na srovnání
- Univerzita:Vysoké učení technické v Brně
- Fakulta:Fakulta elektrotechniky a komunikačních technologií
- Kategorie:Přírodní vědy » Matematika
- Předmět:Matematický seminář
- Studijní obor:-
- Ročník:-
- Formát:PDF dokument (.pdf)
- Rozsah A4:105 stran
2.3 Axiomy, definice, věty a důkazy
Základem logické výstavby matematiky je soubor axiomů, t.j. matematických výroků, které se považují za pravdivé a nedokazují se. K zavedení nových pojmů slouží definice, která stanoví název pojmu a určí jeho základní vlastnosti. Věta v matematice je pravdivý výrok, který musíme logicky odvodit - dokázat - z axiomů, definic a dříve dokázaných vět. Podle použitých postupů rozlišujeme důkaz přímý, nepřímý, důkaz sporem, důkaz matematickou indukcí.
Příklad 2.6 Věta: Součin dvou libovolných sudých Čísel je dělitelný čtyřmi.
Důkaz přímý:
Jde o součin 21 * 2k = 4lk (l,k patří Z) a to bylo dokázat.
Příklad 2.7 Věta: Nechť rovnice ax2 + bx + c = 0 má celočíselné koeficienty, a ^ 0, b je číslo liché. Dokažte, ze rovnice nemůže mít dvojnásobný kořen.
Důkaz sporem:
Předpokládáme, Že rovnice má dvojnásobný kořen. Pak diskriminant je nulový. Víme, že b = 2k + 1, k e Z. Tedy D = (2k + 1)2 - 4ac = 0 => 4fc2 + 4fc + 1 = 4ac. Na levé straně rovnice je liché číslo, na pravé straně sudé a to je spor. Neplatí tedy předpoklad, že kvadratická rovnice má za daných podmínek dvojnásobný kořen.
Příklad 2.8 Matematickou indukcí dokažte, že součet Čtverců prvních n přirozených Čísel je roven Sn = 1/6(n + 1)(2n + 1).
Důkaz:
Matematickou indukcí dokazujeme výrok V(u) tak, Že nejprve dokážeme platnost V{a),
kde a je nejmenší přirozené Číslo pro danou úlohu. Pak předpokládáme platnost V(n) a
ukážeme platnost implikace V(n) ^ V(n+ 1). Pak V(n) platí pro všechna n.
V našem případě:
V{1) : Si = 4 . 1 . 2 . 3 = 1, což odpovídá Si = l2.
Předpokládáme V(n) : Sn = |n(n + l)(2n + 1).
Počítáme V{n + 1) : S(n + 1) = S(n) + (n + l)2 = |n(n + l)(2n + 1) + (n + l)2 =
i(n + l)(2n2 + 7n + 6) = |(n + l)(n + 2)(2n + 3).
Základem logické výstavby matematiky je soubor axiomů, t.j. matematických výroků, které se považují za pravdivé a nedokazují se. K zavedení nových pojmů slouží definice, která stanoví název pojmu a určí jeho základní vlastnosti. Věta v matematice je pravdivý výrok, který musíme logicky odvodit - dokázat - z axiomů, definic a dříve dokázaných vět. Podle použitých postupů rozlišujeme důkaz přímý, nepřímý, důkaz sporem, důkaz matematickou indukcí.
Příklad 2.6 Věta: Součin dvou libovolných sudých Čísel je dělitelný čtyřmi.
Důkaz přímý:
Jde o součin 21 * 2k = 4lk (l,k patří Z) a to bylo dokázat.
Příklad 2.7 Věta: Nechť rovnice ax2 + bx + c = 0 má celočíselné koeficienty, a ^ 0, b je číslo liché. Dokažte, ze rovnice nemůže mít dvojnásobný kořen.
Důkaz sporem:
Předpokládáme, Že rovnice má dvojnásobný kořen. Pak diskriminant je nulový. Víme, že b = 2k + 1, k e Z. Tedy D = (2k + 1)2 - 4ac = 0 => 4fc2 + 4fc + 1 = 4ac. Na levé straně rovnice je liché číslo, na pravé straně sudé a to je spor. Neplatí tedy předpoklad, že kvadratická rovnice má za daných podmínek dvojnásobný kořen.
Příklad 2.8 Matematickou indukcí dokažte, že součet Čtverců prvních n přirozených Čísel je roven Sn = 1/6(n + 1)(2n + 1).
Důkaz:
Matematickou indukcí dokazujeme výrok V(u) tak, Že nejprve dokážeme platnost V{a),
kde a je nejmenší přirozené Číslo pro danou úlohu. Pak předpokládáme platnost V(n) a
ukážeme platnost implikace V(n) ^ V(n+ 1). Pak V(n) platí pro všechna n.
V našem případě:
V{1) : Si = 4 . 1 . 2 . 3 = 1, což odpovídá Si = l2.
Předpokládáme V(n) : Sn = |n(n + l)(2n + 1).
Počítáme V{n + 1) : S(n + 1) = S(n) + (n + l)2 = |n(n + l)(2n + 1) + (n + l)2 =
i(n + l)(2n2 + 7n + 6) = |(n + l)(n + 2)(2n + 3).
Klíčová slova:
symbolika
logika
geometrie
výrazy
proměnná
derivace
axiomy
rovnice
Obsah:
- Obsah
1 Přehled použité symboliky 4
2 Základní pojmy matematické logiky a teorie množin 5
2.1 Elementy matematické logiky 5
2.2 Základní operace s množinami 6
2.3 Axiomy, definice, věty a důkazy 7
3 Vektorová algebra a analytická geometrie 9
3.1 Základní operace s vektory 9
3.2 Přímka v rovině 9
3.3 Přímka v prostoru a rovnice roviny 11
3.4 Kuželosečky v rovině 13
4 Úpravy agebraických výrazů a rovnice 18
4.1 Úpravy agebraických výrazů 18
4.2 Rovnice 20
5 Soustavy rovnic 29
5.1 Soustavy lineárních rovnic 29
5.2 Gaussova eliminační metoda 30
6 Řešení nerovnic 34
0.1 Operace s nerovnicemi 34
6.2 Lineární nerovnice 35
0.3 Kvadratická nerovnice 37
6.4 Nerovnice s absolutními hodnotami 38
0.5 Iracionální nerovnice a soustavy nerovnic 38
7 Elementární funkce 42
7.1 Lineární funkce 42
7.2 Kvadratická funkce 44
7.3 Mocninná funkce 46
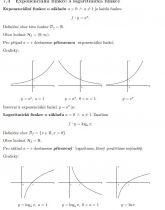
7.4 Exponenciální funkce a logaritmická funkce 50
8 Vlastnosti funkce jedné proměnné 53
8.1 Vlastnosti a druhy funkcí 53
8.2 Inverzní funkce 56
8.3 Limita a spojitost funkce 58
9 Derivace funkce 63
9.1 Geometrický a fyzikální význam derivace 63
9.2 Výpočet derivace 65
9.3 L'Hospitalovo pravidlo 68
10 Goniometrické funkce 70
10.1 Oblouková míra 70
10.2 Goniometrické funkce 71
10.3 Goniometrické rovnice 75
11 Integrál funkce jedné proměnné 78
11.1 Primitivní funkce 78
11.2 Určitý integrál 81
12 Komplexní čísla 86
12.1 Algebraický tvar komplexního čísla 86
12.2 Goniometrický tvar komplexního čísla 87
12.3 Moivreova věta 88
12.4 Řešení binomických rovnic v C 88
13 Posloupnosti a řady 92
13.1 Aritmetická a geometrická posloupnost 92
13.2 Nekonečná geometrická řada 95
14 Kombinatorika 98
14.1 Permutace, variace a kombinace 98
14.2 Binomická veta 100